MATEMÁTICAS II

MATEMATICAS II
Semestre 2013-A

UTILIZA ÁNGULOS, TRIÁNGULOS Y RELACIONES MÉTRICAS.
ÁNGULOS:

Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radian, el grado sexagesimal o el grado centesimal.

CLASIFICACIÓN DE LOS ÁNGULOS POR SU ABERTURA

Agudo: Un ángulo agudo es un ángulo que mide menos de 90°

Recto: Un angulo recto es el que mide exactamente 90°

Obtuso: Un angulo obtuso es un angulo que mide más de 90° pero menos de 180°

Colineal o Llano: Un angulo llano mide 180°. Un ángulo llano cambia de dirección para apuntar en la contraria.

Entrante: Es el ángulo que mide más de 180° pero menos de 360°.

Perigonal: Es el ángulo que mide exactamente 360°.

2.-POR DOS PARALELAS Y UNA SECANTE:

1.-Ángulos exteriores o externos:

En geometría, un ángulo exterior o ángulo externo es el ángulo formado por un lado de un polígono y la prolongación del lado adyacente. En cada vértice de un polígono es posible conformar dos ángulos exteriores, que poseen la misma amplitud. Cada ángulo exterior es suplementario del ángulo interior que comparte el mismo vértice.

2.-Ángulos interiores o internos:                                                                           

En geometría, un ángulo interior o ángulo interno es un ángulo formado por dos lados de un polígono que compartiendo un extremo común, está contenido dentro del polígono. Un polígono simple tiene sólo un ángulo interno por cada vértice y está situado del lado opuesto del polígono.

3.- Interiores Consecutivos: Cuando dos líneas cruzan a otra (que se llama transversal), los pares de ángulos a un lado de la transversal pero entre las líneas se llaman ángulos interiores consecutivos. 

4.- Alternos Externos: Cuando dos líneas cruzan a otra (que se llama transversal), los pares de ángulos en lados opuestos de la transversal pero fuera de las líneas se llaman ángulos alternos externos.

5.- Alternos Internos:

 Cuando dos líneas cruzan a otra (que se llama transversal), los pares de ángulos en lados opuestos de la transversal pero entre las líneas se llaman ángulos alternos internos.

6.- Correspondientes: 

Cuando dos líneas se cruzan con otra (que se llama transversal), los ángulos en las esquinas correspondientes se llaman ángulos correspondientes. En este ejemplo, son ángulos correspondientes: a y e b y f c y g d y h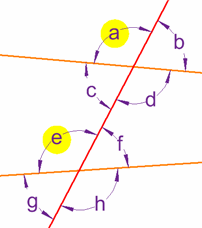

3.-POR LA SUMA DE SUS MEDIDAS

Complementarios: Suman 90°.

Suplementarios: Suman 180°.



TRIÁNGULOS:

Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados, es decir: no colineales). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo.

POR LA MEDIDA DE SUS LADOS

Triángulo equilátero es un triángulo con tres lados congruentes. Ejemplo de un triángulo equilátero: 10cm, 10cm, 10cm. Triángulo isósceles es un triángulo que tiene dos lados congruentes. Ejemplo de un triángulo isósceles: 6cm, 6cm, 8cm.

Triángulo escaleno es un triángulo que no tiene ningún par de lados congruentes.Ejemplo de un triángulo escaleno: 5cm, 7cm, 8cm.

                                            POR LA MEDIDA DE SUS ÁNGULOS

Oblicuángulo: Un triángulo oblicuángulo es aquel que no es recto ninguno de sus ángulos, por lo que no se puede resolver directamente por el teorema de Pitágoras, el triángulo oblicuángulo se resuelve por leyes de senos y de cosenos, así como el que la suma de todos los ángulos internos de un triángulo suman 180 grados.

Obtusángulo: Es el que tiene un ángulo obtuso y dos ángulos agudos. 

Acutángulo: Es es triangulo que tiene todos sus ángulos menores a 90°.